How to find the scalar product of vectors examples. Dot product of vectors: properties, calculation examples, physical meaning
1. Definition and simplest properties. Let's take non-zero vectors a and b and plot them from an arbitrary point O: OA = a and OB = b. The magnitude of the angle AOB is called the angle between vectors a and b and is denoted (a,b). If at least one of the two vectors is zero, then the angle between them is, by definition, considered right. Note that by definition the angle between vectors is not less than 0 and not more than . Moreover, the angle between two non-zero vectors is equal to 0 if and only if these vectors are co-directional and equal to if and only if they are in opposite directions.
Let's check that the angle between the vectors does not depend on the choice of point O. This is obvious if the vectors are collinear. Otherwise, we will postpone from an arbitrary point O 1 vectors O 1 A 1 = a and O 1 IN 1 = b and note that triangles AOB and A 1 ABOUT 1 IN 1 equal on three sides, because |OA| = |O 1 A 1 | = |a|, |OB| = |O 1 IN 1 | = |b|, |AB| = |A 1 IN 1 | = |b–a|. Therefore, angles AOB and A 1 ABOUT 1 IN 1 are equal.
Now we can give the main point in this paragraph
(5.1) Definition. The scalar product of two vectors a and b (denoted ab) is the number 6 , equal to the product of the lengths of these vectors and the cosine of the angle between the vectors. Briefly speaking:
ab = |a||b|cos (a,b).
The operation of finding a scalar product is called scalar vector multiplication. The scalar product aa of a vector with itself is called the scalar square of this vector and is denoted a 2 .
(5.2) The scalar square of a vector is equal to the square of its length.
If |a| 0, then (a,a) = 0, from where a 2 = |a||a|cos0 = |a| 2 . If a = 0, then a 2 = |a| 2 = 0.
(5.3) Cauchy inequality. The modulus of the scalar product of two vectors does not exceed the product of the moduli of the factors: |ab| |a||b|. In this case, equality is achieved if and only if the vectors a and b are collinear.
By definition |ab| = ||a||b|cos (a,b)| = |a||b||cos (a,b)| |a||b. This proves Cauchy's inequality itself. Now let's notice. that for non-zero vectors a and b equality in it is achieved if and only if |cos (a,b)| = 1, i.e. at (a,b) = 0 or (a,b) = . The latter is equivalent to the fact that vectors a and b are co-directed or oppositely directed, i.e. collinear. If at least one of the vectors a and b is zero, then they are collinear and |ab| = |a||b| = 0.
2. Basic properties of scalar multiplication. These include the following:
(SU1) ab = ba (commutativity);
(SU2) (xa)b = x(ab) (associativity);
(SU3) a(b+c) = ab + ac (distributivity).
The commutativity here is obvious, because ab = bа. The associativity at x = 0 is also obvious. If x > 0, then
(ha)b = |ha||b|cos (xa,b) = |x||a||b|cos (xa,b) = x|a||b|cos (a,b) = x(ab),
for (xa,b) = (a,b) (from the co-direction of vectors xa and a - Fig. 21). If x< 0, then
(xa)b = |x||a||b|cos (хa,b) = –х|а||b|(–cos (a,b)) = x|a||b|cos (a,b) = x(ab),
for (xa,b) = – (a,b) (from the opposite direction of the vectors xa and a - Fig. 22). Thus, associativity is also proven.
Proving distributivity is more difficult. For this we need such
(5.4) Lemma. Let a be a nonzero vector parallel to the line l, and b an arbitrary vector. Then the orthogonal projectionb" of the vector b to the straight line l is equal to 
.
1)
<
/2. Then the vectors a and 
co-directed (Fig. 23) and
b"
=
=
=
.
2) > /2. Then the vectors a andb" are oppositely directed (Fig. 24) and
b"
=
–
=
–
=
.
3)
=
/2. Thenb"
=
0 and ab
=
0, from whereb"
=
=
0.
Now we prove distributivity (SU3). It is obvious if vector a is zero. Let a
0. Then we draw the straight line l
||
a, and denote byb" Andc" orthogonal projections of vectors b and c onto it, and throughd" is the orthogonal projection of the vector d = b+c onto it. By Theorem 3.5d"
=
b"+
c"Applying Lemma 5.4 to the last equality, we obtain the equality 
=
. Scalarly multiplying it by a, we find that 
2
=
, from which ad = ab+ac, which is what needed to be proved.
The properties of scalar multiplication of vectors that we have proven are similar to the corresponding properties of multiplication of numbers. But not all properties of multiplication of numbers carry over to scalar multiplication of vectors. Here are typical examples:
1
2) If ab = ac, then this does not mean that b = c, even if vector a is non-zero. Example: b and c are two different vectors of the same length, forming equal angles with vector a (Fig. 25).
3) It is not true that a(bc) = (ab)c is always true: if only because the validity of such an equality for bc, ab 0 implies collinearity of vectors a and c.
3. Orthogonality of vectors. Two vectors are called orthogonal if the angle between them is right. The orthogonality of vectors is indicated by the icon .
When we determined the angle between vectors, we agreed to consider the angle between the zero vector and any other vector to be straight. Therefore, the zero vector is orthogonal to any. This agreement allows us to prove such
(5.5) Test for orthogonality of two vectors. Two vectors are orthogonal if and only if their dot product is 0.
Let a and b be arbitrary vectors. If at least one of them is zero, then they are orthogonal, and their scalar product is equal to 0. Thus, in this case the theorem is true. Let us now assume that both of these vectors are non-zero. By definition ab = |a||b|cos (a,b). Since, according to our assumption, the numbers |a| and |b| are not equal to 0, then ab = 0 cos (a,b) = 0 (a,b) = /2, which is what needed to be proven.
The equality ab = 0 is often taken to determine the orthogonality of vectors.
(5.6) Corollary. If vector a is orthogonal to each of the vectors a 1 , …, A P , then it is orthogonal to any linear combination of them.
It is enough to note that from the equality aa 1 = ... = aa P = 0 follows the equality a(x 1 A 1 + … +x P A P ) = x 1 (ahh 1 ) + … + x P (ahh P ) = 0.
From Corollary 5.6 we can easily derive the school criterion for the perpendicularity of a line and a plane. In fact, let some line MN be perpendicular to two intersecting lines AB and AC. Then the vector MN is orthogonal to the vectors AB and AC. Let us take any straight line DE in the ABC plane. The vector DE is coplanar to the non-collinear vectors AB and AC, and therefore expands along them. But then it is also orthogonal to the vector MN, that is, the lines MN and DE are perpendicular. It turns out that the straight line MN is perpendicular to any straight line from the ABC plane, which is what needed to be proved.
4. Orthonormal bases. (5.7) Definition. A basis of a vector space is called orthonormal if, firstly, all its vectors have unit length and, secondly, any two of its vectors are orthogonal.
Vectors of an orthonormal basis in three-dimensional space are usually denoted by the letters i, j and k, and in the vector plane by the letters i and j. Taking into account the sign of orthogonality of two vectors and the equality of the scalar square of a vector to the square of its length, the conditions for the orthonormality of the basis (i,j,k) of the space V 3 can be written like this:
(5.8)i 2 = j 2 = k 2 = 1, ij = ik = jk = 0,
and the basis (i,j) of the vector plane - like this:
(5.9) i 2 = j 2 = 1, ij = 0.
Let vectors a and b have an orthonormal basis (i,j,k) of the space V 3 coordinates (a 1 , A 2 , A 3 ) and (b 1 b 2 , b 3 ) respectively. Thenab = (A 1 i+A 2 j+A 3 k)(b 1 i+b 2 j+b 3 k) = a 1 b 1 i 2 +a 2 b 2 j 2 +a 3 b 3 k 2 +a 1 b 2 ij+a 1 b 3 ik+a 2 b 1 ji+a 2 b 3 jk+a 3 b 1 ki+a 3 b 2 kj = a 1 b 1 + a 2 b 2 + a 3 b 3 . This is how we get the formula for the scalar product of vectors a(a 1 ,A 2 ,A 3 ) and b(b 1 ,b 2 ,b 3 ), given by their coordinates in the orthonormal basis of space V 3 :
(5.10) ab = a 1 b 1 + a 2 b 2 + a 3 b 3 .
For vectors a(a 1 ,A 2 ) and b(b 1 , b 2 ), given by their coordinates in an orthonormal basis on the vector plane, it has the form
(5.11) ab = a 1 b 1 + a 2 b 2 .
Let's substitute b = a into formula (5.10). It turns out that in an orthonormal basis a 2 = a 1 2 + a 2 2 + a 3 2 . Since a 2 = |a| 2 , we get the following formula for finding the length of the vector a(a 1 ,A 2 ,A 3 ), given by its coordinates in the orthonormal basis of space V 3 :
(5.12) |a| = 
.
On the vector plane, due to (5.11), it takes the form
(5.13) |a| = 
.
Substituting b = i, b = j, b = k into formula (5.10), we obtain three more useful equalities:
(5.14) ai = a 1 , aj = a 2 , ak = a 3 .
The simplicity of coordinate formulas for finding the scalar product of vectors and the length of the vector is the main advantage of orthonormal bases. For non-orthonormal bases, these formulas are, generally speaking, incorrect, and their use in this case is a gross mistake.
5. Direction cosines. Let us take in the orthonormal basis (i,j,k) of the space V 3 vector a(a 1 ,A 2 ,A 3 ). Thenai = |a||i|cos (a,i) = |a|cos (a,i).On the other hand, ai = a 1 according to formula 5.14. It turns out that
(5.15) a 1 = |a|cos (a,i).
and, similarly,
A 2 = |a|cos (a,j), and 3 = |a|cos (a,k).
If the vector a is unit, these three equalities take on a particularly simple form:
(5.16) A 1 =cos (a,i),A 2 =cos (a,j),A 3 =cos (a,k).
The cosines of the angles formed by a vector with the vectors of an orthonormal basis are called the direction cosines of this vector in this basis. As formulas 5.16 show, the coordinates of a unit vector in an orthonormal basis are equal to its direction cosines.
From 5.15 it follows that a 1 2 + a 2 2 + a 3 2 = |a| 2 (cos 2 (a,i)+cos 2 (a,j) +cos 2 (a,k)). On the other hand, a 1 2 + a 2 2 + a 3 2 = |a| 2 . It turns out that
(5.17) the sum of the squares of the direction cosines of a non-zero vector is equal to 1.
This fact can be useful for solving some problems.
(5.18) Problem. The diagonal of a rectangular parallelepiped forms angles of 60 with its two edges emerging from the same vertex. . What angle does it form with the third edge emerging from this vertex?
Consider an orthonormal basis of the space V 3
, whose vectors are depicted by the edges of a parallelepiped extending from a given vertex. Since the diagonal vector forms angles of 60 with two vectors of this basis
, the squares of two of its three direction cosines are equal to cos 2
60
= 1/4. Therefore, the square of the third cosine is equal to 1/2, and this cosine itself is equal to 1/ 
. This means that the required angle is 45
.
Definition 1
The scalar product of vectors is a number equal to the product of the dynes of these vectors and the cosine of the angle between them.
The notation for the product of vectors a → and b → has the form a → , b → . Let's transform it into the formula:
a → , b → = a → · b → · cos a → , b → ^ . a → and b → denote the lengths of the vectors, a → , b → ^ - designation of the angle between given vectors. If at least one vector is zero, that is, has a value of 0, then the result will be equal to zero, a → , b → = 0
When multiplying a vector by itself, we get the square of its length:
a → , b → = a → b → cos a → , a → ^ = a → 2 cos 0 = a → 2
Definition 2
Scalar multiplication of a vector by itself is called a scalar square.
Calculated by the formula:
a → , b → = a → · b → · cos a → , b → ^ .
The notation a → , b → = a → · b → · cos a → , b → ^ = a → · n p a → b → = b → · n p b → a → shows that n p b → a → is the numerical projection of a → onto b → , n p a → a → - projection of b → onto a →, respectively.
Let us formulate the definition of a product for two vectors:
The scalar product of two vectors a → by b → is called the product of the length of the vector a → by the projection b → by the direction of a → or the product of the length b → by the projection a →, respectively.
Dot product in coordinates
The scalar product can be calculated through the coordinates of vectors in a given plane or in space.
The scalar product of two vectors on a plane, in three-dimensional space, is called the sum of the coordinates of given vectors a → and b →.
When calculating the scalar product of given vectors a → = (a x , a y) , b → = (b x , b y) on the plane in the Cartesian system, use:
a → , b → = a x b x + a y b y ,
for three-dimensional space the expression is applicable:
a → , b → = a x · b x + a y · b y + a z · b z .
In fact, this is the third definition of the scalar product.
Let's prove it.
Evidence 1
To prove it, we use a → , b → = a → · b → · cos a → , b → ^ = a x · b x + a y · b y for vectors a → = (a x , a y) , b → = (b x , b y) on Cartesian system.
Vectors should be set aside
O A → = a → = a x , a y and O B → = b → = b x , b y .
Then the length of the vector A B → will be equal to A B → = O B → - O A → = b → - a → = (b x - a x , b y - a y) .
Consider triangle O A B .
A B 2 = O A 2 + O B 2 - 2 · O A · O B · cos (∠ A O B) is correct based on the cosine theorem.
According to the condition, it is clear that O A = a → , O B = b → , A B = b → - a → , ∠ A O B = a → , b → ^ , which means we write the formula for finding the angle between vectors differently
b → - a → 2 = a → 2 + b → 2 - 2 · a → · b → · cos (a → , b → ^) .
Then from the first definition it follows that b → - a → 2 = a → 2 + b → 2 - 2 · (a → , b →) , which means (a → , b →) = 1 2 · (a → 2 + b → 2 - b → - a → 2) .
Applying the formula for calculating the length of vectors, we get:
a → , b → = 1 2 · ((a 2 x + a y 2) 2 + (b 2 x + b y 2) 2 - ((b x - a x) 2 + (b y - a y) 2) 2) = = 1 2 (a 2 x + a 2 y + b 2 x + b 2 y - (b x - a x) 2 - (b y - a y) 2) = = a x b x + a y b y
Let us prove the equalities:
(a → , b →) = a → b → cos (a → , b → ^) = = a x b x + a y b y + a z b z
– respectively for vectors of three-dimensional space.
The scalar product of vectors with coordinates says that the scalar square of a vector is equal to the sum of the squares of its coordinates in space and on the plane, respectively. a → = (a x , a y , a z) , b → = (b x , b y , b z) and (a → , a →) = a x 2 + a y 2 .
Dot product and its properties
There are properties of the dot product that apply to a → , b → and c → :
- commutativity (a → , b →) = (b → , a →) ;
- distributivity (a → + b → , c →) = (a → , c →) + (b → , c →) , (a → + b → , c →) = (a → , b →) + (a → , c →) ;
- combinative property (λ · a → , b →) = λ · (a → , b →), (a → , λ · b →) = λ · (a → , b →), λ - any number;
- scalar square is always greater than zero (a → , a →) ≥ 0, where (a → , a →) = 0 in the case when a → zero.
The properties are explainable thanks to the definition of the scalar product on the plane and the properties of addition and multiplication of real numbers.
Prove the commutative property (a → , b →) = (b → , a →) . From the definition we have that (a → , b →) = a y · b y + a y · b y and (b → , a →) = b x · a x + b y · a y .
By the property of commutativity, the equalities a x · b x = b x · a x and a y · b y = b y · a y are true, which means a x · b x + a y · b y = b x · a x + b y · a y .
It follows that (a → , b →) = (b → , a →) . Q.E.D.
Distributivity is valid for any numbers:
(a (1) → + a (2) → + . . . + a (n) → , b →) = (a (1) → , b →) + (a (2) → , b →) + . . . + (a (n) → , b →)
and (a → , b (1) → + b (2) → + . . + b (n) →) = (a → , b (1) →) + (a → , b (2) →) + . . . + (a → , b → (n)) ,
hence we have
(a (1) → + a (2) → + . . . + a (n) → , b (1) → + b (2) → + . . . + b (m) →) = = (a ( 1) → , b (1) →) + (a (1) → , b (2) →) + . . . + (a (1) → , b (m) →) + + (a (2) → , b (1) →) + (a (2) → , b (2) →) + . . . + (a (2) → , b (m) →) + . . . + + (a (n) → , b (1) →) + (a (n) → , b (2) →) + . . . + (a (n) → , b (m) →)
Dot product with examples and solutions
Any problem of this kind is solved using the properties and formulas relating to the scalar product:
- (a → , b →) = a → · b → · cos (a → , b → ^) ;
- (a → , b →) = a → · n p a → b → = b → · n p b → a → ;
- (a → , b →) = a x · b x + a y · b y or (a → , b →) = a x · b x + a y · b y + a z · b z ;
- (a → , a →) = a → 2 .
Let's look at some example solutions.
Example 2
The length of a → is 3, the length of b → is 7. Find the dot product if the angle has 60 degrees.
Solution
By condition, we have all the data, so we calculate it using the formula:
(a → , b →) = a → b → cos (a → , b → ^) = 3 7 cos 60 ° = 3 7 1 2 = 21 2
Answer: (a → , b →) = 21 2 .
Example 3
Given vectors a → = (1 , - 1 , 2 - 3) , b → = (0 , 2 , 2 + 3) . What is the scalar product?
Solution
This example considers the formula for calculating coordinates, since they are specified in the problem statement:
(a → , b →) = a x · b x + a y · b y + a z · b z = = 1 · 0 + (- 1) · 2 + (2 + 3) · (2 + 3) = = 0 - 2 + ( 2 - 9) = - 9
Answer: (a → , b →) = - 9
Example 4
Find the scalar product of A B → and A C →. Points A (1, - 3), B (5, 4), C (1, 1) are given on the coordinate plane.
Solution
To begin with, the coordinates of the vectors are calculated, since by condition the coordinates of the points are given:
A B → = (5 - 1, 4 - (- 3)) = (4, 7) A C → = (1 - 1, 1 - (- 3)) = (0, 4)
Substituting into the formula using coordinates, we get:
(A B →, A C →) = 4 0 + 7 4 = 0 + 28 = 28.
Answer: (A B → , A C →) = 28 .
Example 5
Given vectors a → = 7 · m → + 3 · n → and b → = 5 · m → + 8 · n → , find their product. m → equals 3 and n → equals 2 units, they are perpendicular.
Solution
(a → , b →) = (7 · m → + 3 · n → , 5 · m → + 8 · n →) . Applying the distributivity property, we get:
(7 m → + 3 n →, 5 m → + 8 n →) = = (7 m →, 5 m →) + (7 m →, 8 n →) + (3 n → , 5 m →) + (3 n → , 8 n →)
We take the coefficient out of the sign of the product and get:
(7 m → , 5 m →) + (7 m → , 8 n →) + (3 n → , 5 m →) + (3 n → , 8 n →) = = 7 · 5 · (m → , m →) + 7 · 8 · (m → , n →) + 3 · 5 · (n → , m →) + 3 · 8 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →)
By the property of commutativity we transform:
35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (m → , n →) + 24 · (n → , n →) = = 35 · (m → , m →) + 71 · (m → , n → ) + 24 · (n → , n →)
As a result we get:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →).
Now we apply the formula for the scalar product with the angle specified by the condition:
(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →) = = 35 · m → 2 + 71 · m → · n → · cos (m → , n → ^) + 24 · n → 2 = 35 · 3 2 + 71 · 3 · 2 · cos π 2 + 24 · 2 2 = 411 .
Answer: (a → , b →) = 411
If there is a numerical projection.
Example 6
Find the scalar product of a → and b →. Vector a → has coordinates a → = (9, 3, - 3), projection b → with coordinates (- 3, - 1, 1).
Solution
By condition, the vectors a → and the projection b → are oppositely directed, because a → = - 1 3 · n p a → b → → , which means the projection b → corresponds to the length n p a → b → → , and with the “-” sign:
n p a → b → → = - n p a → b → → = - (- 3) 2 + (- 1) 2 + 1 2 = - 11 ,
Substituting into the formula, we get the expression:
(a → , b →) = a → · n p a → b → → = 9 2 + 3 2 + (- 3) 2 · (- 11) = - 33 .
Answer: (a → , b →) = - 33 .
Problems with a known scalar product, where it is necessary to find the length of a vector or a numerical projection.
Example 7
What value should λ take for a given scalar product a → = (1, 0, λ + 1) and b → = (λ, 1, λ) will be equal to -1.
Solution
From the formula it is clear that it is necessary to find the sum of the products of coordinates:
(a → , b →) = 1 λ + 0 1 + (λ + 1) λ = λ 2 + 2 λ .
Given we have (a → , b →) = - 1 .
To find λ, we calculate the equation:
λ 2 + 2 · λ = - 1, hence λ = - 1.
Answer: λ = - 1.
Physical meaning of the scalar product
Mechanics considers the application of the dot product.
When A works with a constant force F → a moving body from a point M to N, you can find the product of the lengths of the vectors F → and M N → with the cosine of the angle between them, which means the work is equal to the product of the force and displacement vectors:
A = (F → , M N →) .
Example 8
The movement of a material point by 3 meters under the influence of a force equal to 5 Ntons is directed at an angle of 45 degrees relative to the axis. Find A.
Solution
Since work is the product of the force vector and displacement, it means that based on the condition F → = 5, S → = 3, (F →, S → ^) = 45 °, we obtain A = (F →, S →) = F → · S → · cos (F → , S → ^) = 5 · 3 · cos (45 °) = 15 2 2 .
Answer: A = 15 2 2 .
Example 9
A material point, moving from M (2, - 1, - 3) to N (5, 3 λ - 2, 4) under the force F → = (3, 1, 2), did work equal to 13 J. Calculate the length of movement.
Solution
For given vector coordinates M N → we have M N → = (5 - 2, 3 λ - 2 - (- 1) , 4 - (- 3)) = (3, 3 λ - 1, 7) .
Using the formula for finding work with vectors F → = (3, 1, 2) and M N → = (3, 3 λ - 1, 7), we obtain A = (F ⇒, M N →) = 3 3 + 1 (3 λ - 1) + 2 7 = 22 + 3 λ.
According to the condition, it is given that A = 13 J, which means 22 + 3 λ = 13. This implies λ = - 3, which means M N → = (3, 3 λ - 1, 7) = (3, - 10, 7).
To find the length of movement M N →, apply the formula and substitute the values:
M N → = 3 2 + (- 10) 2 + 7 2 = 158.
Answer: 158.
If you notice an error in the text, please highlight it and press Ctrl+Enter
If in the problem both the lengths of the vectors and the angle between them are presented “on a silver platter,” then the condition of the problem and its solution look like this:
Example 1. Vectors are given. Find the scalar product of vectors if their lengths and the angle between them are represented by the following values:
Another definition is also valid, completely equivalent to definition 1.
Definition 2. The scalar product of vectors is a number (scalar) equal to the product of the length of one of these vectors and the projection of another vector onto the axis determined by the first of these vectors. Formula according to definition 2:
We will solve the problem using this formula after the next important theoretical point.
Definition of the scalar product of vectors in terms of coordinates
The same number can be obtained if the vectors being multiplied are given their coordinates.
Definition 3. The dot product of vectors is a number equal to the sum of the pairwise products of their corresponding coordinates.
On surface
If two vectors and on the plane are defined by their two Cartesian rectangular coordinates
then the scalar product of these vectors is equal to the sum of pairwise products of their corresponding coordinates:
.
Example 2. Find the numerical value of the projection of the vector onto the axis parallel to the vector.
Solution. We find the scalar product of vectors by adding the pairwise products of their coordinates:
Now we need to equate the resulting scalar product to the product of the length of the vector and the projection of the vector onto an axis parallel to the vector (in accordance with the formula).
We find the length of the vector as the square root of the sum of the squares of its coordinates:
.
We create an equation and solve it:
Answer. The required numerical value is minus 8.
In space
If two vectors and in space are defined by their three Cartesian rectangular coordinates
,
then the scalar product of these vectors is also equal to the sum of pairwise products of their corresponding coordinates, only there are already three coordinates:
.
The task of finding the scalar product using the considered method is after analyzing the properties of the scalar product. Because in the problem you will need to determine what angle the multiplied vectors form.
Properties of the scalar product of vectors
Algebraic properties
1. (commutative property: reversing the places of the multiplied vectors does not change the value of their scalar product).
2. 
(associative property with respect to a numerical factor: the scalar product of a vector multiplied by a certain factor and another vector is equal to the scalar product of these vectors multiplied by the same factor).
3. 
(distributive property relative to the sum of vectors: the scalar product of the sum of two vectors by the third vector is equal to the sum of the scalar products of the first vector by the third vector and the second vector by the third vector).
4. (scalar square of vector greater than zero), if is a nonzero vector, and , if is a zero vector.
Geometric properties
In the definitions of the operation under study, we have already touched on the concept of an angle between two vectors. It's time to clarify this concept.
In the figure above you can see two vectors that are brought to a common origin. And the first thing you need to pay attention to is that there are two angles between these vectors - φ 1 And φ 2 . Which of these angles appears in the definitions and properties of the scalar product of vectors? The sum of the considered angles is 2 π and therefore the cosines of these angles are equal. The definition of a dot product includes only the cosine of the angle, and not the value of its expression. But the properties only consider one angle. And this is the one of the two angles that does not exceed π , that is, 180 degrees. In the figure this angle is indicated as φ 1 .
1. Two vectors are called orthogonal And the angle between these vectors is straight (90 degrees or π /2 ), if the scalar product of these vectors is zero :
.
Orthogonality in vector algebra is the perpendicularity of two vectors.
2. Two non-zero vectors make up sharp corner (from 0 to 90 degrees, or, which is the same - less π dot product is positive .
3. Two non-zero vectors make up obtuse angle (from 90 to 180 degrees, or, what is the same - more π /2) if and only if they dot product is negative .
Example 3. The coordinates are given by the vectors:
.
Calculate the scalar products of all pairs of given vectors. What angle (acute, right, obtuse) do these pairs of vectors form?
Solution. We will calculate by adding the products of the corresponding coordinates.
We got a negative number, so the vectors form an obtuse angle.
We got a positive number, so the vectors form an acute angle.
We got zero, so the vectors form a right angle.
We got a positive number, so the vectors form an acute angle.
.
We got a positive number, so the vectors form an acute angle.
For self-test you can use online calculator Dot product of vectors and cosine of the angle between them .
Example 4. Given the lengths of two vectors and the angle between them:
.
Determine at what value of the number the vectors and are orthogonal (perpendicular).
Solution. Let's multiply the vectors using the rule for multiplying polynomials:
Now let's calculate each term:
.
Let’s create an equation (the product is equal to zero), add similar terms and solve the equation:
Answer: we got the value λ = 1.8, at which the vectors are orthogonal.
Example 5. Prove that the vector 
orthogonal (perpendicular) to the vector
Solution. To check orthogonality, we multiply the vectors and as polynomials, substituting instead the expression given in the problem statement:
.
To do this, you need to multiply each term (term) of the first polynomial by each term of the second and add the resulting products:
.
In the resulting result, the fraction is reduced by. The following result is obtained:
Conclusion: as a result of multiplication we got zero, therefore, the orthogonality (perpendicularity) of the vectors is proven.
Solve the problem yourself and then see the solution
Example 6. The lengths of the vectors and are given, and the angle between these vectors is π /4 . Determine at what value μ vectors and are mutually perpendicular.
For self-test you can use online calculator Dot product of vectors and cosine of the angle between them .
Matrix representation of the dot product of vectors and the product of n-dimensional vectors
Sometimes it is advantageous for clarity to represent two multiplied vectors in the form of matrices. Then the first vector is represented as a row matrix, and the second - as a column matrix:
Then the scalar product of vectors will be the product of these matrices :
The result is the same as that obtained by the method we have already considered. We got one single number, and the product of a row matrix by a column matrix is also one single number.
It is convenient to represent the product of abstract n-dimensional vectors in matrix form. Thus, the product of two four-dimensional vectors will be the product of a row matrix with four elements by a column matrix also with four elements, the product of two five-dimensional vectors will be the product of a row matrix with five elements by a column matrix also with five elements, and so on.
Example 7. Find scalar products of pairs of vectors
,
using matrix representation.
Solution. The first pair of vectors. We represent the first vector as a row matrix, and the second as a column matrix. We find the scalar product of these vectors as the product of a row matrix and a column matrix:
We similarly represent the second pair and find:
As you can see, the results were the same as for the same pairs from example 2.
Angle between two vectors
The derivation of the formula for the cosine of the angle between two vectors is very beautiful and concise.
To express the dot product of vectors
(1)
in coordinate form, we first find the scalar product of the unit vectors. The scalar product of a vector with itself by definition:
What is written in the formula above means: the scalar product of a vector with itself is equal to the square of its length. The cosine of zero is equal to one, so the square of each unit will be equal to one:
Since vectors
are pairwise perpendicular, then the pairwise products of the unit vectors will be equal to zero:
Now let's perform the multiplication of vector polynomials:
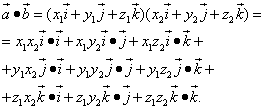
We substitute the values of the corresponding scalar products of the unit vectors into the right side of the equality:
We obtain the formula for the cosine of the angle between two vectors:
Example 8. Three points are given A(1;1;1), B(2;2;1), C(2;1;2).
Find the angle.
Solution. Finding the coordinates of the vectors:
,
.
Using the cosine angle formula we get:
Hence, .
For self-test you can use online calculator Dot product of vectors and cosine of the angle between them .
Example 9. Two vectors are given
Find the sum, difference, length, dot product and angle between them.
2.Difference
Angle between vectors
Consider two given vectors $\overrightarrow(a)$ and $\overrightarrow(b)$. Let us subtract the vectors $\overrightarrow(a)=\overrightarrow(OA)$ and $\overrightarrow(b)=\overrightarrow(OB)$ from an arbitrarily chosen point $O$, then the angle $AOB$ is called the angle between the vectors $\overrightarrow( a)$ and $\overrightarrow(b)$ (Fig. 1).
Picture 1.
Note here that if the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ are codirectional or one of them is the zero vector, then the angle between the vectors is $0^0$.
Notation: $\widehat(\overrightarrow(a),\overrightarrow(b))$
The concept of dot product of vectors
Mathematically, this definition can be written as follows:
The dot product can be zero in two cases:
If one of the vectors is a zero vector (Since then its length is zero).
If the vectors are mutually perpendicular (that is, $cos(90)^0=0$).
Note also that the scalar product is greater than zero if the angle between these vectors is acute (since $(cos \left(\widehat(\overrightarrow(a),\overrightarrow(b))\right)\ ) >0$), and less than zero if the angle between these vectors is obtuse (since $(cos \left(\widehat(\overrightarrow(a),\overrightarrow(b))\right)\ )
Related to the concept of a scalar product is the concept of a scalar square.
Definition 2
The scalar square of a vector $\overrightarrow(a)$ is the scalar product of this vector with itself.
We find that the scalar square is equal to
\[\overrightarrow(a)\overrightarrow(a)=\left|\overrightarrow(a)\right|\left|\overrightarrow(a)\right|(cos 0^0\ )=\left|\overrightarrow(a )\right|\left|\overrightarrow(a)\right|=(\left|\overrightarrow(a)\right|)^2\]
Calculating the dot product from vector coordinates
In addition to the standard way of finding the value of the scalar product, which follows from the definition, there is another way.
Let's consider it.
Let the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ have coordinates $\left(a_1,b_1\right)$ and $\left(a_2,b_2\right)$, respectively.
Theorem 1
The scalar product of the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ is equal to the sum of the products of the corresponding coordinates.
Mathematically this can be written as follows
\[\overrightarrow(a)\overrightarrow(b)=a_1a_2+b_1b_2\]
Proof.
The theorem has been proven.
This theorem has several consequences:
Corollary 1: Vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ are perpendicular if and only if $a_1a_2+b_1b_2=0$
Corollary 2: The cosine of the angle between the vectors is equal to $cos\alpha =\frac(a_1a_2+b_1b_2)(\sqrt(a^2_1+b^2_1)\cdot \sqrt(a^2_2+b^2_2))$
Properties of the scalar product of vectors
For any three vectors and a real number $k$ the following is true:
$(\overrightarrow(a))^2\ge 0$
This property follows from the definition of a scalar square (Definition 2).
Travel law:$\overrightarrow(a)\overrightarrow(b)=\overrightarrow(b)\overrightarrow(a)$.
This property follows from the definition of the scalar product (Definition 1).
Distributive law:
$\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)$. \end(enumerate)
By Theorem 1, we have:
\[\left(\overrightarrow(a)+\overrightarrow(b)\right)\overrightarrow(c)=\left(a_1+a_2\right)a_3+\left(b_1+b_2\right)b_3=a_1a_3+a_2a_3+ b_1b_3+b_2b_3==\overrightarrow(a)\overrightarrow(c)+\overrightarrow(b)\overrightarrow(c)\]
Combination law:$\left(k\overrightarrow(a)\right)\overrightarrow(b)=k(\overrightarrow(a)\overrightarrow(b))$. \end(enumerate)
By Theorem 1, we have:
\[\left(k\overrightarrow(a)\right)\overrightarrow(b)=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow(a)\overrightarrow(b))\]
An example of a problem for calculating the scalar product of vectors
Example 1
Find the scalar product of the vectors $\overrightarrow(a)$ and $\overrightarrow(b)$ if $\left|\overrightarrow(a)\right|=3$ and $\left|\overrightarrow(b)\right|= 2$, and the angle between them is equal to $((30)^0,\ 45)^0,\ (90)^0,\ (135)^0$.
Solution.
Using Definition 1, we get
For $(30)^0:$
\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((30)^0\right)\ )=6\cdot \frac(\sqrt(3))(2)=3\sqrt( 3)\]
For $(45)^0:$
\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((45)^0\right)\ )=6\cdot \frac(\sqrt(2))(2)=3\sqrt( 2)\]
For $(90)^0:$
\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((90)^0\right)\ )=6\cdot 0=0\]
For $(135)^0:$
\[\overrightarrow(a)\overrightarrow(b)=6(cos \left((135)^0\right)\ )=6\cdot \left(-\frac(\sqrt(2))(2)\ right)=-3\sqrt(2)\]
Thus, the length of the vector is calculated as the square root of the sum of the squares of its coordinates 
. The length of an n-dimensional vector is calculated similarly 
. If we remember that each coordinate of a vector is the difference between the coordinates of the end and the beginning, then we obtain the formula for the length of the segment, i.e. Euclidean distance between points.
Scalar product two vectors on a plane is the product of the lengths of these vectors and the cosine of the angle between them: 
. It can be proven that the scalar product of two vectors 
= (x 1, x 2) and 
= (y 1 , y 2) is equal to the sum of the products of the corresponding coordinates of these vectors: 
= x 1 * y 1 + x 2 * y 2 .
In n-dimensional space, the scalar product of vectors X= (x 1, x 2,...,x n) and Y= (y 1, y 2,...,y n) is defined as the sum of the products of their corresponding coordinates: X*Y = x 1 * y 1 + x 2 * y 2 + ... + x n * y n.
The operation of multiplying vectors by each other is similar to multiplying a row matrix by a column matrix. We emphasize that the result will be a number, not a vector.
The scalar product of vectors has the following properties (axioms):
1) Commutative property: X*Y=Y*X.
2) Distributive property with respect to addition: X(Y+Z) =X*Y+X*Z.
3) For any real number 
.
4)
, ifX is not a zero vector; 
ifX is a zero vector.
A linear vector space in which a scalar product of vectors is given that satisfies the four corresponding axioms is called Euclidean linear vectorspace.
It is easy to see that when we multiply any vector by itself, we get the square of its length. So it's different length a vector can be defined as the square root of its scalar square:.
The vector length has the following properties:
1) |X| = 0Х = 0;
2) |X| = ||*|X|, where is a real number;
3) |X*Y||X|*|Y| ( Cauchy-Bunyakovsky inequality);
4) |X+Y||X|+|Y| ( triangle inequality).
The angle between vectors in n-dimensional space is determined based on the concept of a scalar product. In fact, if 
, That 
. This fraction is not greater than one (according to the Cauchy-Bunyakovsky inequality), so from here we can find .
The two vectors are called orthogonal or perpendicular, if their scalar product is equal to zero. From the definition of the scalar product it follows that the zero vector is orthogonal to any vector. If both orthogonal vectors are non-zero, then cos= 0, i.e.=/2 = 90 o.
Let's look again at Figure 7.4. It can be seen from the figure that the cosine of the angle of the inclination of the vector to the horizontal axis can be calculated as 
, and the cosine of the angleinclination of the vector to the vertical axis is as 
. These numbers are usually called direction cosines. It is easy to verify that the sum of the squares of the direction cosines is always equal to one: cos 2 +cos 2 = 1. Similarly, the concepts of direction cosines can be introduced for spaces of higher dimensions.
Vector space basis
For vectors, we can define the concepts linear combination,linear dependence And independence similar to how these concepts were introduced for matrix rows. It is also true that if the vectors are linearly dependent, then at least one of them can be expressed linearly in terms of the others (i.e., it is a linear combination of them). The converse is also true: if one of the vectors is a linear combination of the others, then all these vectors together are linearly dependent.
Note that if among the vectors a l , a 2 ,...a m there is a zero vector, then this set of vectors is necessarily linearly dependent. In fact, we get l a l + 2 a 2 +...+ m a m = 0 if, for example, we equate the coefficient j at the zero vector to one, and all other coefficients to zero. In this case, not all coefficients will be equal to zero ( j ≠ 0).
In addition, if some part of the vectors from a set of vectors are linearly dependent, then all of these vectors are linearly dependent. In fact, if some vectors give a zero vector in their linear combination with coefficients that are not both zero, then the remaining vectors multiplied by the zero coefficients can be added to this sum of products, and it will still be a zero vector.
How to determine whether vectors are linearly dependent?
For example, let's take three vectors: a 1 = (1, 0, 1, 5), a 2 = (2, 1, 3, -2) and a 3 = (3, 1, 4, 3). Let's create a matrix from them, in which they will be columns:
Then the question of linear dependence will be reduced to determining the rank of this matrix. If it turns out to be equal to three, then all three columns are linearly independent, and if it turns out to be less, then this will indicate a linear dependence of the vectors.
Since the rank is 2, the vectors are linearly dependent.
Note that the solution to the problem could also begin with reasoning that is based on the definition of linear independence. Namely, create a vector equation l a l + 2 a 2 + 3 a 3 = 0, which will take the form l *(1, 0, 1, 5) + 2 *(2, 1, 3, -2) + 3 *(3, 1, 4, 3) = (0, 0, 0, 0). Then we get a system of equations:
Solving this system using the Gaussian method will be reduced to obtaining the same step matrix, only it will have one more column - free terms. They will all be zero, since linear transformations of zeros cannot lead to a different result. The transformed system of equations will take the form:
The solution to this system will be (-с;-с; с), where с is an arbitrary number; for example, (-1;-1;1). This means that if we take l = -1; 2 =-1 and 3 = 1, then l a l + 2 a 2 + 3 a 3 = 0, i.e. the vectors are actually linearly dependent.
From the solved example it becomes clear that if we take the number of vectors greater than the dimension of space, then they will necessarily be linearly dependent. In fact, if we took five vectors in this example, we would get a 4 x 5 matrix, the rank of which could not be greater than four. Those. the maximum number of linearly independent columns would still not be more than four. Two, three or four four-dimensional vectors can be linearly independent, but five or more cannot. Consequently, no more than two vectors can be linearly independent on the plane. Any three vectors in two-dimensional space are linearly dependent. In three-dimensional space, any four (or more) vectors are always linearly dependent. And so on.
That's why dimension space can be defined as the maximum number of linearly independent vectors that can be in it.
A set of n linearly independent vectors of an n-dimensional space R is called basis this space.
Theorem. Each vector of linear space can be represented as a linear combination of basis vectors, and in a unique way.
Proof. Let the vectors e l , e 2 ,...e n form a basis-dimensional space R. Let us prove that any vector X is a linear combination of these vectors. Since, together with vector X, the number of vectors will become (n +1), these (n +1) vectors will be linearly dependent, i.e. there are numbers l , 2 ,..., n ,, not simultaneously equal to zero, such that
l e l + 2 e 2 +...+ n e n +Х = 0
In this case, 0, because otherwise we would get l e l + 2 e 2 +...+ n e n = 0, where not all coefficients l , 2 ,..., n are equal to zero. This means that the basis vectors would be linearly dependent. Therefore, we can divide both sides of the first equation by:
( l /)e l + ( 2 /)e 2 +...+ ( n /)e n + X = 0
Х = -( l /)e l - ( 2 /)e 2 -...- ( n /)e n
Х = x l e l +x 2 e 2 +...+x n e n,
where x j = -( j /), 
.
Now we prove that such a representation in the form of a linear combination is unique. Let's assume the opposite, i.e. that there is another representation:
Х = y l e l +y 2 e 2 +...+y n e n
Let us subtract from it term by term the previously obtained expression:
0 = (y l – x 1)e l + (y 2 – x 2)e 2 +...+ (y n – x n)e n
Since the basis vectors are linearly independent, we obtain that (y j - x j) = 0, 
, i.e. y j = x j . So the expression turned out to be the same. The theorem has been proven.
The expression X = x l e l +x 2 e 2 +...+x n e n is called decomposition vector X based on e l, e 2,...e n, and numbers x l, x 2,...x n - coordinates vector x relative to this basis, or in this basis.
It can be proven that if nnonzero vectors of an n-dimensional Euclidean space are pairwise orthogonal, then they form a basis. In fact, let's multiply both sides of the equality l e l + 2 e 2 +...+ n e n = 0 by any vector e i. We get l (e l *е i) + 2 (e 2 *е i) +...+ n (e n *е i) = 0 i (e i *е i) = 0 i = 0 for i.
Vectors e l , e 2 ,...e n of n-dimensional Euclidean space form orthonormal basis, if these vectors are pairwise orthogonal and the norm of each of them is equal to one, i.e. if e i *e j = 0 for i≠j и |е i | = 1 fori.
Theorem (no proof). In every n-dimensional Euclidean space there is an orthonormal basis.
An example of an orthonormal basis is a system of n unit vectors e i , for which the i-th component is equal to one and the remaining components are equal to zero. Each such vector is called ort. For example, the vector vectors (1, 0, 0), (0, 1, 0) and (0, 0, 1) form the basis of three-dimensional space.