High and low pass filters (pass filter). Active filters Bandpass filters on transistors
An electrical filter is a device for transmitting electrical signals that passes currents in a certain frequency range and prevents them from passing outside this range. In radio engineering and electronics, electrical filters are divided into passive and active. Passive filter circuits contain only passive elements: resistors, capacitors and inductors.
In addition to the indicated elements, active filter circuits include active products such as transistors or integrated circuits. The filtering properties of a device are determined by its amplitude-frequency characteristic, which is the dependence of the gain of this device on the signal frequency. In a certain frequency range, called the passband or transparency band, electrical oscillations are transmitted by the filter from input to output with virtually no attenuation. Outside the transparency band is an attenuation or delay band, within which the frequency components of the signal are attenuated. Between the transparency band and the stopband there is a frequency called the cutoff frequency. Due to the fact that there is a smooth transition between the transparency band and the attenuation band, the limiting frequency is usually considered to be the frequency at which the signal attenuation is equal to -3 dB - that is, the voltage is √2 times less than in the transparency band.
It is always interesting to get a steep transition in the amplitude-frequency response between the transparency band and the attenuation band. In passive filters, increasing the steepness of such a transition is achieved by complicating the circuit and using multi-link systems. Complex filters require cumbersome calculations and fine tuning. Thanks to the use of feedback, active filters are much simpler and cheaper.
It is customary to divide filters into four categories depending on the location of the transparency band:
. low pass filters (0 ≤ f ≤ f 0);
. high pass filters (f ≥ f 0);
. bandpass filters (f 01 ≤ f ≤ f 02);
. stop or notch filters (0 ≤ f ≤ f 01 and f ≥ f 02).
Here f is the frequency of signals passing through the filter; f 0 - cut-off frequency; f 01 - lower limit frequency; f 02 - upper limit frequency. Thus, a low-pass filter nponycks the signal components whose frequency is less than the cutoff frequency; a high-pass filter passes signal components whose frequency is greater than the cutoff frequency; a bandpass filter passes signal components whose frequency is between the lower limit frequency f 01 and the upper limit frequency f 02; Finally, the notch filter attenuates signals whose frequency is between the lower limit f 01 and the upper limit f 02 frequencies. There are also more complex filters for special purposes, such as the comb filter used in color television, which passes many narrow bands and attenuates the gaps between them.
Electric filters are widely used in electrical engineering, radio engineering and electronics. Thus, a low-pass filter is used at the output of the rectifiers, passing only the direct component of the rectified current and weakening the passage of ripples. In radio receivers, bandpass filters are widely used, which make it possible to select from the signals of many radio stations received by the antenna only one, the frequency band of which falls within the transparency band of the filter.
Another common division of all filters is into two categories: filters whose circuit contains inductors, and filters without inductors, RC filters or resistor-capacitor filters.
Active RC filters have a huge advantage over their passive counterparts, especially at frequencies below 10 kHz. Passive filters for low frequencies must contain large inductors and large capacitors. Therefore, they turn out to be bulky, expensive, and their characteristics are far from ideal.
High inductance is achieved due to the large number of turns of the coil and the use of a ferromagnetic core. This deprives it of the properties of pure inductance, since the long wire of a multi-turn coil has noticeable resistance, and the ferromagnetic core is subject to the influence of temperature on its magnetic properties. The need to use a large capacitance forces the use of capacitors with poor stability, for example electrolytic ones. Active filters are largely free from these disadvantages.
Differentiator and integrator circuits, built using operational amplifiers, are the simplest active filters. When choosing circuit elements in a certain dependence on frequency, the differentiator becomes a high-pass filter, and the integrator becomes a low-pass filter. Next we will look at examples of other more complex and more versatile filters. A large number of other possible active filter schemes, along with their detailed mathematical analysis, can be found in various textbooks and manuals.

Low Pass Filters
By combining an inverting amplifier circuit with an integrator circuit, a first-order low-pass filter circuit is formed, which is shown in rice. 1.
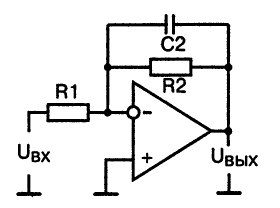
Rice. 1.
Such a filter is an inverting amplifier with a constant gain in the transparency band from direct current to the cutoff frequency f 0 . It can be seen that within the transparency band, as long as the capacitance of the capacitor is sufficiently large, the gain of the circuit coincides with the gain of the inverting amplifier:

The cutoff frequency of this filter is determined by the elements of the feedback circuit in accordance with the expression:

Amplitude-frequency characteristic - the dependence of the signal amplitude at the output of a device on frequency at a constant amplitude at the input of this device - is presented in Fig.2.
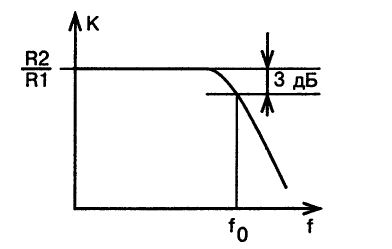
Rice. 2
In the attenuation band above the cutoff frequency f 0, the gain decreases with an intensity of 20 dB/decade (or 6 dB/octave), which means a decrease in the voltage gain by 10 times with an increase in frequency also by 10 times, or a decrease in the gain by half for each doubling the frequency.
If such a steep slope of the amplitude-frequency response in the attenuation band is not enough, you can use a second-order low-pass filter, the circuit of which is shown in Fig.3.

Rice. Z
The gain of the second-order low-pass filter is the same as that of the first-order filter, due to the fact that the total resistance of the resistors in the inverse input circuit, as before, is expressed by the value of R1:
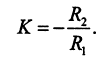
The cutoff frequency when the condition R 1 C 1 = 4R 2 C 2 is fulfilled is also expressed by the same formula:

As for the amplitude-frequency response of this filter, presented in rice. 4, then it is characterized by an increased slope, which is 12 dB/octave.

Rice. 4
Thus, in the attenuation band, as the frequency doubles, the signal voltage at the filter output decreases fourfold.
High Pass Filters
A high-pass filter circuit is constructed in a similar way, which is presented in Fig.5. Such a filter is an inverting amplifier with a constant gain in the transparency band from frequency f0 and more. In the transparency band, the gain of the circuit is the same as that of the inverting amplifier:

Fig.5. Schematic diagram of an active first-order high-pass filter
The cutoff frequency f 0 at the level of -3 dB is set by the input circuit in accordance with the expression:

The slope of the amplitude-frequency characteristic, which is presented in Fig.6, in the region of the cutoff frequency is 6 dB/octave.
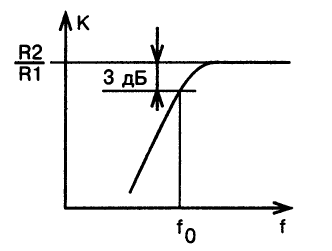
Fig.6. Frequency response of a first-order high-pass filter
As with low-pass filters, a second-order active high-pass filter can be assembled for increased signal rejection in the attenuation band. The schematic diagram of such a filter is shown in Fig.7.

Fig.7. Schematic diagram of an active second-order high-pass filter
The slope of the amplitude-frequency response of the second-order high-pass filter in the region of the cutoff frequency is 12 dB/octave, and the response itself is shown in Fig.8.

Fig.8. Amplitude-frequency response of a second-order high-pass filter
Bandpass filters
If you combine an active low-pass filter with an active high-pass filter, the result is a bandpass filter, the circuit diagram of which is shown in Fig.9.

Rice. 9 . Schematic diagram of an active bandpass filter
This circuit is sometimes called a selective feedback amplifier. Like amplifiers containing oscillating circuits, a bandpass filter also has an amplitude-frequency response with a pronounced maximum at a certain frequency. Such a frequency cannot be called resonant, since resonance is possible only in circuits formed by inductance and capacitance. In other cases, the frequency of such a maximum is usually called the quasi-resonance frequency. For the bandpass filter under consideration, the quasi-resonance frequency f0 is determined by the elements of the feedback circuit:

The frequency response of this bandpass filter is shown in rice. 10.

Fig.10. Amplitude-frequency response of a bandpass filter
The maximum gain at the quasi-resonance frequency turns out to be equal to:

Relative bandwidth at -3 dB:

A schematic diagram of another bandpass filter is shown in rice. eleven.

Rice. eleven. Schematic diagram of a double T filter bandpass filter
Here, a double T-filter formed by resistors R2, R3, R5 and capacitors Cl, C2, SZ is included in the negative feedback circuit.
As you know, if the following conditions are met:
The amplitude-frequency response of a double T-filter contains a quasi-resonance, the frequency of which is equal to

Moreover, at the quasi-resonance frequency, the transmission coefficient of the double T-filter is zero. Therefore, an active filter with a double T filter included in the negative feedback circuit is a bandpass filter with a maximum amplitude-frequency response at the quasi-resonance frequency. Three such characteristics are presented in rice. 12. The characteristics differ in different resistances of the resistor R4: the lower one corresponds to R4 = 100 kOhm, the middle one - R4 = 1 MOhm, the upper one - R4 = ∞.

Rice. 12. Frequency response of an active filter with a double T-filter in a negative feedback circuit
Notch filters
The same double T filter can be included not in the negative feedback circuit, as is done when creating a bandpass filter, but in the input signal circuit. This creates an active notch filter, the diagram of which is shown in rice, 13.

Fig.13. Schematic diagram of a double T filter notch filter
If the previous conditions are met
The amplitude-frequency characteristic of an active filter that has a double T filter in the input circuit contains a quasi-resonance, the frequency of which is still determined by formula (8). But at the quasi-resonance frequency, the gain of this active filter is zero. The frequency response of an active filter with a double T filter in the input circuit is shown in Fig.14.

Rice. 14. Frequency response of an active filter with a double T filter in the input circuit
Complex filters
Several active filters can be connected in series to obtain a frequency response with increased slope. In addition, sections of simple filters connected in series have reduced sensitivity. This means that a small deviation in the magnitude of one of the circuit components (deviation in resistor value or capacitor value from the norm) will lead to less impact on the final filter response than in the case of a similar complex filter built on a single op-amp.

Rice. 15. Schematic diagram of a step filter
On rice. 15 shows a step filter assembled from three operational amplifiers. The popularity of such filters has increased sharply after the appearance on sale of integrated circuits containing several operational amplifiers in one package. The advantages of this filter are low sensitivity to deviations in component values and the ability to obtain three outputs: high frequencies U out1, bandpass U out2 and low frequencies U out3.
The filter is composed of a summing amplifier DA1 and two integrators DA2, DA3, which are connected in the form of a closed loop. If the circuit elements are selected according to the condition ![]()
then the cutoff frequency turns out to be equal
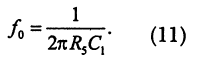
The outputs of the high and low frequencies have a slope of the amplitude-frequency response equal to 12 dB/octave, and the bandpass output has a triangular characteristic with a maximum at frequency f 0 with a quality factor Q, which is determined by the resistors of the gain setting of the DA1 microcircuit.
Frequency filters are the simplest electrical circuits whose frequency response is nonlinear. The resistance in such circuits changes as the signal frequency changes. Such a circuit may consist of one or more circuit elements.
Passive and active low pass filters
A passive filter consists of resistors or capacitors only. They do not require energy to perform the tasks assigned to them. Almost all passive filters have a linear response.

An active filter includes a transistor or operational amplifier in its design. The frequency response of such a filter is more favorable than that of a passive one.

The question is, why and where are they used? Filters operate on the following principle: the signal received by them is filtered, and only those signals that are necessary remain. One of the areas of application of such devices is electronic color music.

Characteristics of frequency filters
The frequency at which the amplitude of the output signal decreases to a value of 0.7 from the input is called the cutoff frequency.

The slope of the frequency response of the filter. It shows how dramatically the signal changes after it has passed the filter. The larger the angle, the better.






Types of frequency filters
- Single element;
- G, T, U-shaped;
- Multi-star. They are series-connected L-shaped.

This article will discuss the circuits and design of a low-pass filter.

The simplest do-it-yourself low-pass filter
It is quite possible to make this device at home and its quality will not be much inferior to its store-bought counterpart. In addition, the low cost and simplicity of the design will pay off all the efforts invested.

What will be the characteristics
- Cutoff frequency – 300 Hz. The transmitted signal will not be higher than this indicator;
- Required voltage –9/30 V;
- Electricity consumption – 7 mA.

What you need to make a low pass filter:
- DD1 BA4558;
- VD1 D814B;
- C1, C2 10 µF;
- C3 0.033 µF;
- C4 220 nf;
- C5 100 nf;
- C6 100 µF;
- C7 10 µF;
- C8 100 nf;
- R1, R2 15 kOhm;
- R3, R4 100 kOhm;
- R5 47 kOhm;
- R6, R7 10 kOhm;
- R8 1 kOhm;
- R9 100 kOhm - variable;
- R10 100 kOhm;
- R11 2 kOhm.

Instructions on how to make a simple filter correctly
In a circuit that includes resistor R11, capacitor C6, and stabilizer VD1, a unit is assembled that stabilizes the incoming voltage. If the supplied voltage is less than 15 V, the resistor must be removed from the circuit.

Elements R1, R2, C1, C2 are adders of incoming signals. If the filter is fed with a mono signal, the adder can be removed. After this, you need to connect the signal source directly to the next (second) contact.






DD1.1 is an amplifier of the incoming signal, and DD1.2 contains a device that does not transmit high signals.


PCB manufacturing
We have described the circuit that needs to be used, now we will manufacture the most important element, namely the printed circuit board.

You need to take fiberglass, the width of which should be 2 cm and the length 4 cm. First, degrease the surface and sand it thoroughly. Then, after printing the diagram below, transfer it to a piece of fiberglass, observing the dimensions. It is recommended to use the LUT method.
Note! 

The design should be completely imprinted on the surface of the workpiece; if you did not succeed in doing this the first time, you can finish drawing the interrupted paths by hand.

We prepare a solution in which we will etch fiberglass. You need to take 2 tablespoons of citric acid and 6 tablespoons of hydrogen peroxide and mix them thoroughly. To speed up the mixing process, add a pinch of salt to the alkaline solution. Salt does not participate in the dissolution process.

You need to place the prepared workpiece with the drawn paths directly into the resulting solution. Before diving, make sure that the track pattern is well drawn, otherwise you will ruin the surface.

After waiting a little, make sure that all the excess copper layer has dissolved. Then you need to remove the workpiece from the container and rinse it in running water. Using acetone, remove ink from the board.

Assembly
In order to avoid mistakes during soldering, it is advisable to use a diagram. Solder all elements sequentially and carefully.
Note! 






Conclusion
The scheme described above should work after the first turn on. The filter does not require any settings. The main problems that may arise during startup are associated with poor-quality assembly or soldering, and in rare cases, with a malfunction of the circuit elements used.

In some cases, there is no sound after turning on the filter. To fix the problem you need to turn the variable resistor knob. If this does not help, check all connections at the solder points.

Photos of low pass filters






Note! 













Active filters are implemented using amplifiers (usually op-amps) and passive RC filters. Among the advantages of active filters compared to passive ones, the following should be highlighted:
· lack of inductors;
· better selectivity;
· compensation for the attenuation of useful signals or even their amplification;
· suitability for implementation in the form of an IC.
Active filters also have disadvantages:
¨ energy consumption from the power source;
¨ limited dynamic range;
¨ additional nonlinear signal distortions.
We also note that the use of active filters with op-amps at frequencies above tens of megahertz is difficult due to the low unity gain frequency of most widely used op-amps. The advantage of active filters on op-amps is especially evident at the lowest frequencies, down to fractions of hertz.
In the general case, we can assume that the op-amp in the active filter corrects the frequency response of the passive filter by providing different conditions for the passage of different frequencies of the signal spectrum, compensates for losses at given frequencies, which leads to steep drops in the output voltage on the slopes of the frequency response. For these purposes, various frequency-selective feedback loops are used in op-amps. Active filters ensure that the frequency response of all types of filters is obtained: low pass (LPF), high pass (HPF) and band pass (PF).
The first stage of the synthesis of any filter is to specify a transfer function (in operator or complex form), which meets the conditions of practical feasibility and at the same time ensures the required frequency response or phase response (but not both) of the filter. This stage is called filter characteristic approximation.
The operator function is a ratio of polynomials:
K( p)=A( p)/B( p),
and is uniquely determined by zeros and poles. The simplest numerator polynomial is a constant. The number of poles of the function (and in active filters on an op-amp, the number of poles is usually equal to the number of capacitors in the circuits that form the frequency response) determines the order of the filter. The order of the filter indicates the decay rate of its frequency response, which for the first order is 20 dB/dec, for the second - 40 dB/dec, for the third - 60 dB/dec, etc.
The approximation problem is solved for a low-pass filter, then using the frequency inversion method, the resulting dependence is used for other types of filters. In most cases, the frequency response is set, taking the normalized transmission coefficient:
![]() ,
,
where f(x) is the filtering function; - normalized frequency; - filter cutoff frequency; e is the permissible deviation in the passband.
Depending on which function is taken as f(x), filters (starting from the second order) of Butterworth, Chebyshev, Bessel, etc. are distinguished. Figure 7.15 shows their comparative characteristics.

The Butterworth filter (Butterworth function) describes the frequency response with the most flat part in the passband and a relatively low decay rate. The frequency response of such a low-pass filter can be presented in the following form:
where n is the filter order.
The Chebyshev filter (Chebyshev function) describes the frequency response with a certain unevenness in the passband, but not a higher decay rate.
The Bessel filter is characterized by a linear phase response, as a result of which signals whose frequencies lie in the passband pass through the filter without distortion. In particular, Bessel filters do not produce emissions when processing square-wave oscillations.
In addition to the listed approximations of the frequency response of active filters, others are known, for example, the inverse Chebyshev filter, Zolotarev filter, etc. Note that the active filter circuits do not change depending on the type of frequency response approximation, but the relationships between the values of their elements change.
The simplest (first order) HPF, LPF, PF and their LFC are shown in Figure 7.16.
In these filters, the capacitor that determines the frequency response is included in the OOS circuit.
For a high-pass filter (Figure 7.16a), the transmission coefficient is equal to:
 ,
,
The frequency of conjugation of asymptotes is found from the condition, from where
![]() .
.
For the low-pass filter (Figure 7.16b) we have:
 ,
,
![]() .
.
The PF (Figure 7.16c) contains elements of a high-pass filter and a low-pass filter.

You can increase the slope of the LFC rolloff by increasing the order of the filters. Active low-pass filters, high-pass filters and second-order filter filters are shown in Figure 7.17.
The slope of their asymptotes can reach 40 dB/dec, and the transition from low-pass filter to high-pass filter, as can be seen from Figures 7.17a, b, is carried out by replacing resistors with capacitors, and vice versa. The PF (Figure 7.17c) contains high-pass filter and low-pass filter elements. The transfer functions are equal:
¨ for low-pass filter:
 ;
;
¨ for high-pass filter:

 .
.
For PF, the resonant frequency is equal to:
 .
.
For low-pass filter and high-pass filter, the cutoff frequencies are respectively equal to:
![]() ;
;
![]() .
.
Quite often, second-order PFs are implemented using bridge circuits. The most common are double T-shaped bridges, which “do not pass” the signal at the resonance frequency (Figure 7.18a) and Wien bridges, which have a maximum transmission coefficient at the resonant frequency (Figure 7.18b).

Bridge circuits are included in the PIC and OOS circuits. In the case of a double T-bridge, the feedback depth is minimal at the resonance frequency, and the gain at this frequency is maximum. When using a Wien bridge, the gain at the resonance frequency is maximum, because maximum depth of POS. At the same time, to maintain stability, the depth of the OOS introduced using resistors and must be greater than the depth of the POS. If the depths of the POS and OOS are close, then such a filter can have an equivalent quality factor Q»2000.
Resonant frequency of a double T-bridge at and ![]() , and the Wien Bridge
, and the Wien Bridge ![]() And
And ![]() , is equal
, is equal ![]() , and it is chosen based on the stability condition
, and it is chosen based on the stability condition ![]() , because The transmission coefficient of the Wien bridge at frequency is 1/3.
, because The transmission coefficient of the Wien bridge at frequency is 1/3.
To obtain a notch filter, a double T-shaped bridge can be connected as shown in Figure 7.18c, or a Wien bridge can be included in the OOS circuit.
To build an active tunable filter, a Wien bridge is usually used, whose resistors are made in the form of a dual variable resistor.
It is possible to construct an active universal filter (LPF, HPF and PF), a circuit version of which is shown in Figure 7.19.

It consists of an op-amp adder and two first-order low-pass filters on the op-amp and , which are connected in series. If ![]() , then the coupling frequency
, then the coupling frequency ![]() . The LFC has a slope of asymptotes of the order of 40 dB/dec. The universal active filter has good stability of parameters and high quality factor (up to 100). In serial ICs, a similar principle of constructing filters is often used.
. The LFC has a slope of asymptotes of the order of 40 dB/dec. The universal active filter has good stability of parameters and high quality factor (up to 100). In serial ICs, a similar principle of constructing filters is often used.
Gyrators
A gyrator is an electronic device that converts the impedance of reactive elements. Typically this is a capacitance-to-inductance converter, i.e. equivalent to inductance. Sometimes gyrators are called inductance synthesizers. The widespread use of gyrators in ICs is explained by the great difficulties in manufacturing inductors using solid-state technology. The use of gyrators makes it possible to obtain a relatively large inductance with good weight and size characteristics.
Figure 7.20 shows an electrical diagram of one of the options for a gyrator, which is an op-amp repeater covered by a frequency-selective PIC ( and ).

Since the capacitance of the capacitor decreases with increasing signal frequency, the voltage at the point A will increase. Along with it, the voltage at the output of the op-amp will increase. The increased voltage from the output through the PIC circuit is supplied to the non-inverting input, which leads to a further increase in voltage at the point A, and the more intense, the higher the frequency. Thus, the voltage at the point A behaves like the voltage across an inductor. The synthesized inductance is determined by the formula:
![]() .
.
The quality factor of a gyrator is defined as:
![]() .
.
One of the main problems when creating gyrators is the difficulty in obtaining the equivalent of an inductance in which both terminals are not connected to a common bus. Such a gyrator is performed on at least four op-amps. Another problem is the relatively narrow range of operating frequencies of the gyrator (up to several kilohertz for widely used op amps).
Make your own subwoofer filter
Making your own filter for a subwoofer is not as difficult as it seems at first glance. The decision to make it yourself does not come easily.
Sooner or later, all car audio enthusiasts become professionals and try in every way to improve the audio system. The simplest low-pass filter for a subwoofer and its manufacture will become one of the modernization solutions.
Purpose
Beyond the boundaries of the “native” band (effectively reproduced), the sound pressure coming from the speaker noticeably decreases and at the same time the level of distortion increases. In this case, it is simply stupid to talk about some kind of sound quality and, therefore, in order to solve the problem, you have to use several speakers in the audio system (see).
This is the reality: this happens in both home acoustics and car audio. That's not news.
Typical speaker layouts in cars and the role of filters
Regarding car acoustics, I would like to highlight two typical schemes for constructing a sound system, which are probably familiar to everyone who is not very familiar with car audio.
We are talking about the following schemes:
- The most popular scheme involves three speakers. This is a woofer (aimed exclusively at the lows), a mid- and low-frequency speaker (midbass) and a tweeter responsible for high-frequency reproduction.
Note. This circuit is used mostly by amateurs and can be found in any car where the acoustic circuit is properly used.
- The following scheme is for more professionals and participants in car audio competitions. Here, a separate speaker is responsible for each of the frequency ranges.
Note. Despite the significant differences, both schemes obey the same rule: each speaker is responsible for reproducing its own frequency band and does not affect others.
It is precisely in order not to violate this requirement that electrical filters are designed, the role of which is to isolate specific “native” frequencies and suppress “foreign” ones.
Filter types
- A notch filter is the exact opposite of a bandpass filter. Here, the band that the PF passes through without changes is suppressed, and bands outside this interval are enhanced;
- FINCH or infra-low frequency suppression filter stands apart. The principle of its operation is based on the suppression of high frequencies with a low cutoff rate (10-30Hz). The purpose of this filter is to directly protect the bass player.
Note. The combination of several filters is called a crossover in acoustics.
Options
In addition to the types of filters, it is customary to separate their parameters.
For example, a parameter such as order indicates the number of coils and capacitors (reactive elements):
- 1st order contains only one element;
- 2nd order two elements, etc.
Another, no less important indicator is the slope of the frequency response, which shows how sharply the filter suppresses “alien” signals.
For subwoofer
In principle, any filter, including this one, is a combination of several elements. These components have the property of selectively transmitting signals of certain frequencies.
It is customary to separate three popular schemes for this separator for the bass player.
They are presented below:
- The first scheme involves the simplest separator (which is not difficult to make with your own hands). It is designed as an adder and uses one transistor.
Of course, serious sound quality cannot be achieved with such a simple filter, but due to its simplicity, it is perfect for amateurs and novice radio enthusiasts;
- The other two schemes are much more complex than the first. Elements built according to these circuits are placed between the signal output point and the input of the bass amplifier.
Whatever the separator, simple or complex, it must have the following technical characteristics.
A simple filter for a 2-way amplifier
This separator does not require any special setup and assembly is as easy as pie. It was performed using available op-amps.
Note. This filter circuit has one slight advantage over the others. It lies in the fact that when the low-frequency channel is overloaded, its distortions are well masked by the mid/high-frequency link and, therefore, the negative load on hearing is noticeably reduced.
Let's get started:
- We apply the input signal to the input of the operational amplifier MC1 (it performs the function of an active low-pass filter);
- We also feed the signal to the input of the MC2 amplifier (in this case, we are talking about a differential amplifier);
- We now apply the signal from the output of low-pass filter MS1 to the input of MS2.
Note. Thus, in MS2, the low-frequency part of the signal (input) is subtracted from the spectrum, and the high-frequency part of the signal appears at the output.
- We provide the specified cutoff frequency of the low-pass filter, which will become the crossover frequency.
The process of making a filter with your own hands will require familiarization with the thematic video review. In addition, it will be useful to study detailed photos - materials, diagrams, other instructions and much more.
The cost of making and installing a filter yourself is minimal, because there are practically no expenses required.
Good day, dear readers! Today we will talk about assembling a simple low-pass filter. But despite its simplicity, the quality of the filter is not inferior to store-bought analogues. So let's get started!
Main characteristics of the filter
- Cutoff frequency 300 Hz, higher frequencies are cut off;
- Supply voltage 9-30 Volts;
- The filter consumes 7 mA.
Scheme
The filter circuit is shown in the following figure:
Parts List:
- DD1 - BA4558;
- VD1 - D814B;
- C1, C2 - 10 µF;
- C3 - 0.033 µF;
- C4 - 220 nf;
- C5 - 100 nf;
- C6 - 100 µF;
- C7 - 10 µF;
- C8 - 100 nf;
- R1, R2 - 15 kOhm;
- R3, R4 - 100 kOhm;
- R5 - 47 kOhm;
- R6, R7 - 10 kOhm;
- R8 - 1 kOhm;
- R9 - 100 kOhm - variable;
- R10 - 100 kOhm;
- R11 - 2 kOhm.
Making a Low Pass Filter
A voltage stabilization unit is assembled using resistor R11, capacitor C6 and zener diode VD1.
If the supply voltage is less than 15 Volts, then R11 should be excluded.
The input signal adder is assembled on components R1, R2, C1, C2.

It can be excluded if a mono signal is supplied to the input. In this case, the signal source should be connected directly to the second pin of the microcircuit.
DD1.1 amplifies the input signal, and DD1.2 directly assembles the filter itself.

Capacitor C7 filters the output signal, a sound control is implemented on R9, R10, C8, it can also be excluded and the signal can be removed from the negative leg of C7.
We've figured out the circuit, now let's move on to making the printed circuit board. For this we need fiberglass laminate measuring 2x4 cm.
Low Pass Filter Board File:
(downloads: 420)

Sand the surface to a shine with fine-grained sandpaper and degrease the surface with alcohol. We print this drawing and transfer it to the textolite using the LUT method.


If necessary, paint the paths with varnish.
Now you should prepare a solution for etching: dissolve 1 part of citric acid in three parts of hydrogen peroxide (proportion 1:3, respectively). Add a pinch of salt to the solution; it is a catalyst and is not involved in the etching process.
We immerse the board in the prepared solution. We are waiting for the excess copper to dissolve from its surface. At the end of the etching process, we take out our board, rinse it with running water and remove the toner with acetone.

Solder the components using this photo as a guide:

In the first version of the drawing, I did not make a hole for R4, so I soldered it from below; this defect is eliminated in the download document.
On the back side of the board you need to solder a jumper:
